

首先,我不是太理解提问者的问题,智能优化算法和机器学习算法是两种不一样的算法,智能优化算法的本质就是做优化的,就像最早的单纯形法,梯度下降法,牛顿法,一样,是做问题的优化,但是,最近几年也有研究者把智能优化算法做分类,做回归这些领域,但是总的来说,智能算法本职就是优化算法。机器学习算法有很多了,各种机器学习算法百花齐放,只要能做一些回归,分类,聚类这些具有学习的事情,都可以认为是机器学习算法,就像有些做智能算法来做分类,也可以称为机器学习算法。机器学习算法热门的有:线性分类回归,对数几率回归,岭回归,支持向量机,决策树,贝叶斯分类器,等等。智能算法也有很多:粒子群,鲸鱼优化算法,模拟退火,等等,太多了,不一一列举了,什么烟花算法,头脑风暴法,飞蛾算法,细菌算法,各种各样
首先楼上说得很对,机器学习和智能优化没啥关系。
我想你应该是想找这些:
1. 模糊逻辑算法
2. 神经网络算法
3. 免疫算法
4. 内分泌算法
5. 人工代谢算法
6. 膜计算
7. 禁忌搜索算法
8. 和声搜索算法
9. 思维进化算法
10. 社会进化算法
11. 人口迁移算法
12. 标杆学习算法
13. 瞭望算法
14. 视觉认知优化算法
15. 头脑风暴优化算法
16. 随机聚焦搜索优化算法
17. 教学优化算法
18. 帝国竞争算法
19. 世界杯竞赛算法
20. 集体决策优化算法
21. 遗传算法
22. 遗传编程
23. 进化规划
24. 进化策略
25. 分布估计算法
26. 差分进化算法
27. DNA计算
28. 基因表达式编程算法
29. Memetic算法
30. 文化算法
31. 蚁群优化算法/蚁狮优化算法
32. 粒子群优化算法
33. 人工蜂群算法/蜂群优化算法
34. 混合蛙跳算法
35. 人工鱼群算法
36. 大马哈鱼洄游算法
37. 鲸鱼优化算法
38. 磷虾群算法
39. 细菌觅食优化算法
40. 细菌(群体)趋药性算法
41. 细菌菌落优化算法
42. 猫群优化算法
43. 鼠群优化算法
44. 猫鼠种群算法
45. 鸡群优化算法
46. 狼群算法
47. 灰狼优化算法
48. 狮子优化算法
49. 猴群算法
50. 雁群优化算法
51. 候鸟优化算法
52. 布谷鸟搜索算法
53. 萤火虫群优化算法/萤火虫算法
54. 飞蛾扑火优化算法
55. 蝙蝠算法
56. 果蝇优化算法
57. 群居蜘蛛优化算法
58. 蟑螂优化算法
59. 捕食搜索算法
60. 自由搜索算法
61. 食物链算法
62. 共生生物搜索算法
63. 生物地理学优化算法
64. 竞争优化算法
65. 模拟植物生长算法
66. 人工植物优化算法
67. 人工藻类算法
68. 小树生长算法
69. 自然树生长竞争算法
70. 根树优化算法
71. 森林优化算法
72. 入侵草优化算法
73. 种子优化算法
74. 花朵授粉算法
75. 模拟退火算法
76. 混沌优化算法
77. 混沌黄金分割搜索算法
78. 随机分形搜索算法
79. 量子搜索算法
80. 智能水滴优化算法
81. 水循环算法
82. 水波优化算法
83. 人工雨滴算法
84. 云搜索优化算法
85. 气象云模型优化算法
86. 风驱动优化算法
87. 宇宙大爆炸算法
88. 中心引力优化算法
89. 引力搜索算法
90. 引力场算法
91. 极值动力学优化算法
92. 拟态物理学优化算法
93. 分子动理论优化算法
94. 类电磁机制算法
95. 热传递搜索算法
96. 涡流搜索算法
97. 闪电搜索算法
98. 光线优化算法
99. 化学反应优化算法
100. 正弦余弦算法
101. 阴阳对优化算法
102. 一维元胞自动机的涌现计算
103. Conway生命游戏的涌现计算
104. 蚂蚁系统觅食路径的涌现计算
105. 数字人工生命Autolife的涌现行为
106. 黏菌的铁路网络涌现计算
来自:李士勇 李 研 林永茂 编著. 智能优化算法与涌现计算
公众号:将门创投 (thejiangmen)
近年来,随着机器学习的兴起和神经网络模型的广泛使用,如何高效训练神经网络使之收敛成为了非常重要的课题。AdaGrad、Adam等自适应梯度优化算法也正是因为有较快的收敛性而在实践中备受青睐,然而并没有一种理论观点得以解释他们能够带来加速的原因。
我“门”有幸邀请到字节跳动AI Lab研究员——黄训蓬来到将门TechBeat,为我们带来Talk“如何利用高阶信息加速优化算法”。
在本次分享中,黄训蓬从理论和实践两个角度说明了自适应梯度优化算法和高阶优化的千丝万缕的联系。
1. Second Moment Matrices如何加速神经网络训练
2. 如何高效精确估计目标函数Hessian矩阵
3. 自适应梯度算法的理论进展
? Talk已在将门TechBeat上线!【点击这里】,即可马上免费观看!

自60年代早期以来,许多群优化算法被引入,从进化算法到灰狼优化等。所有这些算法都显示了它们解决许多优化问题的潜力。本文对一些著名的优化算法进行了梳理研究。
群体智能(Swarm Intelligence, SI)已经引起了各个领域许多研究者的兴趣。Bonabeau将SI定义为“简单代理群体的突发集体智能”[1]。SI是自组织和分散系统的集体智能行为,例如,简单agent的人工群体。例如群居昆虫的群体觅食、合作运输、群居昆虫的筑巢、集体分类和聚类。自组织和劳动分工被认为是科学探究的必要属性。自组织被定义为系统在没有任何外部帮助的情况下将其代理或组件演化成适当形式的能力。Bonabeau et al.[1]也指出,自组织依赖于正反馈、负反馈、波动和多重交互的四个基本性质。正反馈和负反馈分别用于放大和稳定。同时,波动对随机性也很有用。当蚁群在其搜索区域内彼此共享信息时,就会发生多重交互。科学探究的第二个属性是劳动分工,它被定义为个体同时执行各种简单而可行的任务。这种分工使得蜂群能够解决复杂的问题,而这些问题需要个体协同工作。
遗传算法(GA)是由John Holland在1975年提出的[2,3],是一种基于自然选择过程机制的搜索优化算法。该算法的基本概念是模仿“适者生存”的概念;它模拟了在一个自然系统中观察到的过程,强者倾向于适应和生存,而弱者倾向于死亡。GA是一种基于群体的方法,其中群体中的成员根据其解决方案的适合度进行排名。在遗传算法中,通过交叉、繁殖和突变等特定的遗传算子形成新的种群[4-7]。种群可以用一组字符串(称为染色体)表示。在每一代中,一个新的染色体(群体的一个成员)是利用来自前一个群体的最适染色体的信息产生的[4-6]。遗传算法生成可行解的初始种群,并以某种方式将其重新组合,以引导其搜索到搜索空间中更有前途的区域。每一个可行的解决方案都被编码为染色体,也被称为基因型,每一条染色体都将通过适应度函数(评估或目标函数)获得一个适应度度量。染色体的适应度函数的值决定了其生育后代的能力。适应度值越高,最大化问题的解越好;适应度值越低,最小化问题的解越好。基本的遗传算法有五个主要组成部分:随机数生成器、适应度评估单元、复制过程、交叉过程和突变操作。繁殖选择种群中最适的候选者,而交叉则是将最适的染色体结合并传递优良基因给下一代的过程,突变则改变染色体中的一些基因[4-7]。
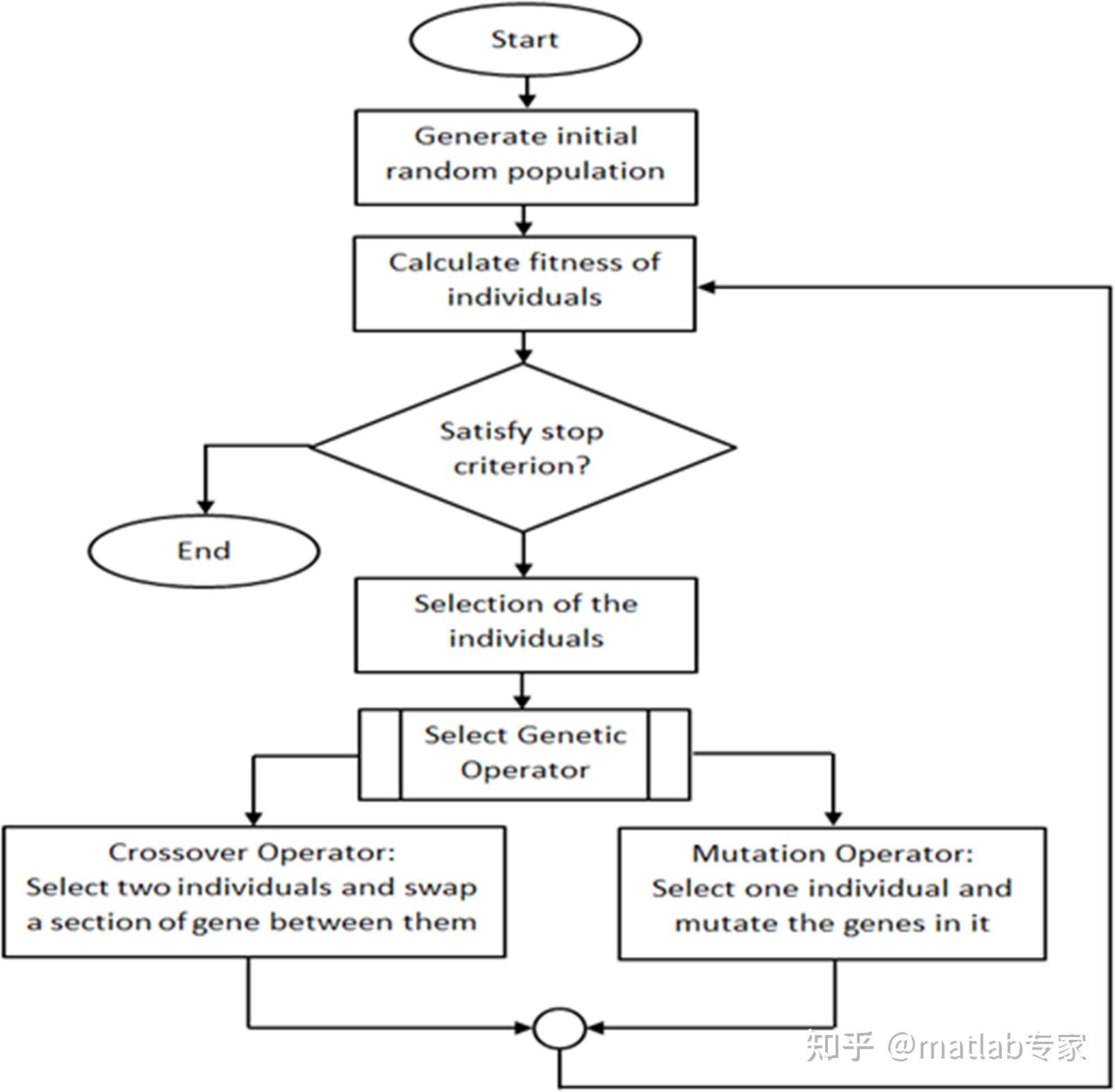
图1给出了遗传算法的总体流程图以及对整个算法的主要组成部分。GA的操作开始于确定一个初始种群,无论是随机的还是使用一些启发式。适应度函数用来评估人口中的成员,然后根据表现对他们进行排名。一旦种群的所有成员已被评估,低秩染色体被省略和其余种群用于繁殖。这是GA最常用的方法之一。另一种可能的选择方案是使用伪随机选择,允许低秩染色体有机会被选择进行繁殖。交叉步骤随机选择剩余种群中的两个成员(最适染色体),并交换和交配它们。遗传算法的最后一步是变异。在这一步中,突变算子在染色体的一个基因上随机突变。变异是遗传算法中至关重要的一步,因为它保证了问题空间的每个区域都能被到达。在交叉和变异操作中,精英主义被用来防止种群的最优解被破坏。精英主义保证了新一代的健康状况至少和现在这一代一样好。新种群的评价和生成一直进行下去,直到达到最大代数或找到最优解。遗传算法的优势在于需要有限的参数设置和初始化自己从可能的解决方案,而不是一个单一的解决方案。遗传算法的一个主要缺点是由于交叉和变异过程是随机的,不能快速收敛到最优值[6,7]。GA的应用范围广泛,从调度[8,9],机器学习[10],机器人[11,12],信号处理[13],商业[14],数学[15],制造[16,17],路由[18],等等。
自遗传算法引入以来,许多研究者都进行了改进遗传算法性能的研究。他们引入了几种交叉和变异的替代方法,以提高解决方案的质量。在交叉中,De Jong等人(1992)和ü?oluk(2002)引入了n点交叉和分段交叉,即选择多个点进行交叉[19,20],而不是选择一个交叉点。它们的区别在于n点交叉是随机选择多个断点,而分段交叉只使用两个断点。突变是遗传算法中最重要的操作符之一,它可以引导染色体走向更好的解。因此,一些研究给出了不同的突变方法。默认情况下,染色体中的每个基因都被赋予概率pm,并根据概率发生突变。这种突变被称为均匀突变。其他的突变方法是位倒位,即使用随机突变[19]使染色体中的整个基因发生突变。引入自适应遗传算法是为了允许在设置种群大小、交叉概率和变异概率时使用精确的参数。所有这些参数都是动态的,并且在迭代过程中不断变化。例如,如果种群没有改善,突变率在增加,当种群改善时,突变率开始下降[21]。Raja和Bhaskaran[22]提出了一种新的GA初始化方法,提高了GA的整体性能。在这种方法中,他们使用两次初始化,第一次初始化用于识别有希望的区域。第一次初始化后,对所有的染色体进行排序,选出最优的染色体。在此之后,GA在已确定的最佳染色体区域内再次初始化。
2. 蚁群优化ACO
蚁群优化(Ant Colony Optimization, ACO)是受Marco Dorigo 1992年博士论文《蚁系统(Ant System, AS)》启发而提出的一种元启发式方法[23-25]。它的灵感来自于真实蚂蚁的觅食行为。该算法由四个主要部分组成(蚂蚁、信息素、守护进程和分散控制),它们对整个系统做出贡献。蚂蚁是一种假想的媒介,用来模拟对搜索空间的探索和开发。在现实生活中,信息素是一种化学物质,由蚂蚁在行进的道路上传播,由于蒸发作用,信息素的强度随着时间的推移而变化。蚁群算法中蚂蚁在搜索空间中移动时会释放信息素,这些信息素的数量反映了蚂蚁的路径强度。蚂蚁根据高强度的路径来选择方向。trail的强度可以被认为是系统的全局内存。Daemon动作用于收集单个蚂蚁无法完成的全局信息,并使用这些信息来确定是否需要添加额外的信息素来帮助收敛。为了使算法在动态环境中具有鲁棒性和灵活性,采用了分散控制。在蚁群算法中,拥有一个分散系统的重要性是由于这样的系统在面对蚂蚁丢失或蚂蚁失败时提供了灵活性。这些基本的组成部分促成了一种合作的交互,从而导致最短路径的出现[23,24]。
与其他进化方法相比,蚁群算法有许多优点,包括提供正反馈从而快速找到解,以及分布式计算避免了过早收敛。这些都是在利用现有的群体代理的集体互动之外的[26,27]。然而,与其他启发式算法相比,蚁群算法的收敛速度较慢,并且缺乏一个集中的处理器来引导蚁群算法得到较好的解。虽然收敛是有保证的,但收敛时间是不确定的。蚁群算法的另一个重要缺点是它在大搜索空间下的性能较差[26,27]。蚁群算法已应用于各种优化问题,如旅行商问题[28]、二次分配问题[29]、车辆路径问题[30]、网络模型问题[31,32]、图像处理问题[33]、移动机器人路径规划问题[34]、无人机系统路径优化问题[35]、项目管理问题[36]等。
许多蚁群算法的变种已经被创造出来,目的是提高整体性能。在蚁群算法引入两年后,Dorigo和Gambardella对蚁群算法的三个主要方面(信息素、状态转移规则和局部搜索过程)进行了改进,产生了蚁群算法的变体——蚁群系统(Ant Colony System, ACS)[37]。
ACS采用集中化(全局)更新方法进行信息素更新,只将搜索集中在迄今为止发现的最佳解决方案的邻域内,以提高收敛时间的效率。状态转移规则不同于蚁群算法,蚁群算法有一个给定的概率(q0)来决定蚂蚁使用哪种行为。q0通常设置为0.9,并与q的值(0≤q≤1)进行比较。如果q的值小于这个值,则使用剥削行为,反之亦然。在局部搜索过程中,将基于边缘交换策略(如2-opt、3-opt或Lin-Kernighan)的局部优化启发式算法应用于蚂蚁生成的每个解,以获得其局部最小值。这种结合了新的信息素管理、新的状态转移和局部搜索的方法,产生了一种求解TSP问题的可变蚁群算法[37]。最大最小蚂蚁系统(MMAS)被认为是蚁群算法的另一个重要变种。该方法由Stutzle和Hoos于2000年提出,它将信息素trail值限制在[τmin, τmax][38]区间内。MMAS还对蚁群算法的三个方面进行了改进。首先,将信息素路径设置为最大值,使蚂蚁的探索行为升级;第二,引入τmin, τmax的时间间隔,限制信息素轨迹以避免停滞。第三,只允许一只蚂蚁添加信息素,以帮助挖掘算法执行过程中发现的最佳解决方案。信息素可以通过使用迭代最佳方法或全局最佳方法添加。在迭代-最优方法中,每次迭代只有具有最优解的蚂蚁添加信息素,而在全局-最优方法中,具有最优解的蚂蚁可以在同一迭代[38]中不考虑其他蚂蚁添加信息素。
3. 粒子群优化PSO
粒子群优化(PSO)是Kennedy和Eberhart在1995年[39]提出的一种优化技术。它使用一种简单的机制,模仿鸟类和鱼群的群体行为,引导粒子寻找全局最优解。Del Valle和他的合著者[40]用分离、对齐和内聚三种简单行为描述PSO,分别如图3所示。分离是避开拥挤的局部同伴的行为,对齐是向局部同伴的平均方向移动的行为。凝聚力是指向当地同伴的平均位置移动的行为。
通过搜索整个高维问题空间,粒子群算法被证明是一种有效的优化算法。它是一种基于群体运动和智能的稳健随机优化方法。它将社会互动的概念应用到问题解决中,没有使用被优化问题的梯度,因此不需要优化问题是微分的,而经典优化方法[42]要求的是微分的。利用粒子群优化算法可以确定具有噪声和随时间变化的不规则问题的优化[43-45]。粒子群算法的参数包括粒子个数、agent在解空间中的位置、agent的速度和邻域(拓扑通信)。
PSO算法首先初始化种群。第二步是计算每个粒子的适应度值,更新个体和全局最佳值,更新粒子的速度和位置。重复第二步至第四步,直到满足终止条件[40,46 - 48]。在第一次迭代中,为了找到最佳的解决方案(探索),所有的粒子都分散开来。对每个粒子进行计算。根据邻域拓扑找到最优解,并更新群体中每个成员的个人和全局最优粒子。通过将所有粒子吸引到具有最佳解的粒子上来实现收敛。
粒子群算法具有许多优点。该算法实现简单,需要设置的参数少,全局搜索有效,对设计变量的缩放不敏感,易于并行化并发处理[48-50]。粒子群算法在中间最优点有快速和过早收敛的倾向,在精细化搜索区域收敛缓慢(局部搜索能力较弱)[48-50]。PSO用于组网[51]、电力系统[52]、信号处理[53]、控制系统[54]、机器学习[55]、图像处理[56-58]等。
一般来说,有几种方法可以用来改进粒子群算法。人口规模是一个重要因素。更高的种群规模可以增加更快和精确收敛的机会。第二种方法是在勘探和开发之间取得平衡。在迭代开始时,高度的探索会给找到接近全局最优解的机会。同时,在迭代接近尾声的时候,大量的开发将使粒子有机会在有希望的区域内找到最精确的解。子群算法是另一种提高粒子群算法基本性能的方法。为每个子群分配不同的任务或目标也可以提高粒子群算法在多目标问题[59]中的效率。另一种提高粒子群算法性能的方法是设置速度方程的贡献分量(动态速度调整)。这种方法可以引导粒子向不同的方向运动,从而更快地收敛到全局最优[60]。
粒子群算法中两个最显著的变体是引入惯性权重和收缩因子。惯性权重(w)是在首次引入粒子群算法(PSO) 3年后,Shi和Eberhart引入的,目的是调节先前速度的影响,同时控制粒子的勘探和开采行为[61]。如果w值较高,则步长较大,导致勘探行为的发生。如果w值较低,则步长较小,就会发生剥削行为。该单元已被公认为基本粒子群算法速度方程的新标准形式。
惯性权的引入提高了粒子群算法在收敛速度和求解质量方面的整体性能。在此基础上,研究了惯性权的最优配置,以优化收敛速度和解的质量。Bratton和Kennedy建议使用大于1.0的惯性权重值,最终降低到低于1.0的值,目的是鼓励早期勘探,并在最后发现最佳区域进行开发[62]。Clerc和Kennedy后来引入了名为K的约束因子,以增加收敛的机会,避免粒子离开搜索空间[63]。
这两种变体都改善了粒子群算法的整体性能。Eberhart和Shi对这两种变体进行了比较,得出了压缩PSO比改进的基本PSO性能更好的结论[64]。粒子群算法中有几个要素,如群通信拓扑结构和粒子的数量,这些要素决定了求解的质量。Figueirdo和Ludermir评估了全局、局部、冯诺伊曼、wheel和四个集群的五种通信拓扑。他们的结论是,与其他拓扑相比,全局拓扑显示出了很好的结果[65]。Bratton和Kennedy研究了粒子数对求解的影响。他们的研究表明,不存在适用于所有优化问题的绝对群体规模数[62]。
4. 差分进化(DE)算法
差分进化(DE)算法是一种基于种群的算法,由于采用了相似的运算符,可以认为与遗传算法相似;交叉、变异和选择。DE和GA的主要区别在于构造更好的解决方案,其中DE依赖于变异操作,而GA依赖于交叉操作。该算法由Storn和Price在1997年提出[66]。由于该算法依赖于变异操作,它利用变异作为一种搜索机制,利用选择操作将搜索指向搜索空间中的潜在区域。目标向量、突变向量和Trail向量是DE用于迭代生成新种群的三个属性。目标向量是包含搜索空间解的向量;突变载体为目标载体的突变;轨迹向量是目标向量与突变向量交叉运算后的合成向量。如前所述,DE算法的基本步骤与GA相似,只有细微差别[67,68]。DE首先执行一些步骤,例如种群初始化,然后求值,以确定种群中最适合的成员。然后,将两个总体向量的加权差与第三个向量相加,得到新的参数向量。这一步被称为突变。在交叉过程中,向量被混合,算法进行最后一步的选择。为了了解DE和GA之间的区别,需要对DE中的三个主要操作符进行更详细的讨论。
在DE中,总体中的所有解都有相同的概率被选择为父母,而不考虑它们的适合度值。这是DE和GA在操作上的主要区别。简单地说,生成的子向量(trail vector)仅在进行变异和交叉操作后才计算。然后,将该子向量的性能与其父向量进行比较,较优的子向量保留在种群中。当式6中两个解向量的差值较小时,就会发生开采行为,当两个解向量的差值较大时,就会发生勘探行为。DE在增强局部搜索能力和保持种群多样性方面具有优势,但收敛缓慢且不稳定[68]。DE被用于各种应用,如电气工程[69]、图像处理[70]、机器学习[71]和经济[72]。
一般来说,DE性能可以通过增加种群大小来改进。它还可以平衡探索和开发行为,即比例因子(决定步长)在迭代开始时较高,在迭代结束时降低。另一个可以使用的步骤是引入精英主义,它可以避免在下一代诞生时最好的解决方案被摧毁。自从Storn和Price引入DE以来,DE有很多变体。Mezura-Montes等人讨论了DE的几种变体,并对它们进行了比较研究[73]。讨论的变量是DE/rand/1/bin、DE/rand/1/exp、DE/best/1/bin、DE/best/1/exp、DE/current-to-best/1、DE/current-to-rand/1、DE/current-to-rand/1/bin和DE/rand/2/dir。它们之间的差异在于选择突变的个体、选择的解决方案对数以及重组的类型[74]。在研究中,DE的变量用DE/x/y/z的形式来描述,其中x表示要摄动的基向量的弦;例如,rand表示随机选择向量产生突变值,best表示群体中选择最佳向量产生突变值。Y是用来生成新向量的向量个数,用整数形式表示,表示用于生成新解的解对的个数。Z表示交叉的类型,例如bin和exp (bin表示二项式,exp表示指数)。同时,current-to-best和current-to-rand是Price[75]提出的算法重组,以消除具有旋转不变量的二项式和指数交叉算子。
5. 人工蜂群算法ABC
人工蜂群算法(Artificial Bee Colony, ABC)是一种最新的群体智能算法。它是由Dervis Karaboga在2005年提出的[76];2007年,对作业成本法的绩效进行了分析[77],得出的结论是,与其他几种方法相比,作业成本法的绩效较好。这个算法的灵感来自于真正的蜜蜂在寻找食物来源(即花蜜)方面的智能行为,以及在蜂巢中与其他蜜蜂分享有关食物来源的信息。该算法被认为与PSO和DE一样简单,易于实现[78]。在该方法中,人工智能主体被定义为三种类型,即被雇佣的蜜蜂、旁观的蜜蜂和侦察的蜜蜂。为了完成算法的过程,每只蜜蜂都被分配了不同的任务。被雇佣的蜜蜂专注于食物来源,并在记忆中保留食物来源的位置。雇佣的蜜蜂的数量等于食物来源的数量,因为每只雇佣的蜜蜂都与一个且只有一个食物来源有关。旁观的蜜蜂从蜂巢中被雇佣的蜜蜂那里接收到食物来源的信息。之后,人们会选择其中一种食物来源来采集花蜜。侦察蜂负责寻找新的食物来源和花蜜。ABC法的一般流程及每一步的详细情况见[76-78]:
ABC的优点包括易于实现、健壮和高度灵活。该算法只需要最大循环数和蚁群大小两个控制参数,具有很高的灵活性。因此,添加和删除蜜蜂不需要重新初始化算法。与其他搜索技术相比,它需要的控制参数更少[77-80]。ABC的缺点包括需要对新参数进行新的适应度测试以提高性能,在串行处理中使用时速度相当慢,需要大量的目标函数评估[81]。ABC已被应用于各个领域,包括工程设计问题[882,83]、网络[84]、商务[85]、电子[86]、调度[86]和图像处理[86]。
ABC算法的引入虽然还不到十多年,但已有相当多的变体可供选择。其中一个重要的ABC变体是交互式ABC (Interactive ABC,简称IABC),旨在解决数值优化问题[87]。Bao和Zeng介绍了围观蜜蜂对食物来源的三种选择策略,它们形成了三种变体,分别是秩选择策略ABC (RABC)、竞赛选择策略ABC (TABC)和破坏选择策略ABC (DABC)[88]。所有这些变异的主要目的是提高种群多样性,避免过早收敛。Bao和Zeng用标准ABC对这些改进的ABC进行了测试,结果表明这三种选择策略比标准ABC具有更好的搜索效果[88]。
6. 萤火虫群优化GSO
Glow worm Swarm Optimization 是Krishnanad和Ghose在2005年提出的一种基于si的多模态函数优化新技术[89,90]。GSO使用称为萤火虫的物理实体(代理)。萤火虫m在时刻t的条件有三个主要参数:搜索空间中的位置(xm(t))、荧光素水平(lm(t))和邻域范围(rm(t))。这三个参数随时间变化[89-91]。首先萤火虫随机分布在工作空间中,而不是像蚁群算法那样随机放置有限区域在搜索区域中。稍后,使用预定义的常量初始化其他参数。然而,类似于其他方法,三个阶段重复,直到满足终止条件。这些阶段是荧光素水平更新、萤火虫移动和邻居范围更新[89].
GSO在传感器范围有限的应用中是有效的,能够检测多个源,并适用于数值优化任务[89-91]。但也存在精度低、收敛速度慢的问题[92,93]。GSO已经应用于路由[94]、群机器人[95]、图像处理[96]和定位[97,98]等问题。
一般来说,可以通过考虑以下修改来改进GSO。1)扩大邻里范围,包括所有代理商。一旦确定了最佳解决方案,所有agent都可以向具有最佳解决方案的agent移动。这一步可以提高开发效率,因为更多的代理是在最好的解决方案范围内。2)为了提高GSO的收敛速度,邻域范围内考虑的邻域数目需要尽可能小。这一步骤可减少GSO所花的时间,因为确定其移动的概率和方向所需的计算量较少。
GSO有几个变体可以提高GSO的整体性能。例如,He等[99]引入了Improved GSO (IGSO),利用对混沌行为的积分来避免局部最优,提高收敛速度和精度。他等人在六个基准函数上测试了他们的算法,结果表明IGSO优于GSO[99]。Zhang等[100]提出了两种提高GSO性能的思路。首先,他们提出了几种改变萤火虫步长的方法,如固定步长、动态线性递减和动态非线性递减[100]。他们比较了步长方法的方差,结果表明动态线性和非线性递减方法都优于固定步长方法。其次,他们提出了GSO的自我探索行为。在这个变体中,他们建议给每只萤火虫分配一个阈值,萤火虫和它的邻居的适应度值应该大于这个值。如果没有,萤火虫需要在随机螺旋搜索和随机z形搜索中随机选择,以找到更好的适应度值。如果适应度值大于阈值,则使用基本的GSO算法[100]。Zhao等人[101]在GSO中引入了一种局部搜索算子,以提高收敛精度和效率[101]。
7. 布谷鸟搜索算法CSA
布谷鸟搜索算法(CSA)是Yang和Deb在2009年提出的一种最新的元启发式方法[102]。该算法的灵感来自布谷鸟物种的行为,如巢内寄生虫,以及Lévy航班的特征,如一些鸟类和果蝇。CSA在其实施中使用三个基本规则或操作。首先,每只杜鹃每次迭代只允许产一枚蛋,杜鹃随机选择巢产卵。其次,高质量的蛋和巢会被传给下一代。第三,可利用的主巢数量是固定的,杜鹃的蛋被宿主鸟发现,概率为paavium[0,1]。换句话说,宿主可以选择是扔掉蛋,还是放弃巢,完全建立一个新巢。最后的假设可以近似为一个分数,pa的总n个巢被一个新的随机解替换。该算法还可以扩展到更复杂的点,每个巢包含多个蛋[102,103]。在这三个主要规则的基础上,讨论了CSA中采取的步骤的细节。
与其他方法相比,CSA具有多模态目标函数的优点,需要微调的参数数量较少。它对参数pa也具有不敏感的收敛速度,在某些情况下无需对参数进行微调[102-104]。CSA应用于多个领域,包括神经网络[105]、嵌入式系统[106]、电磁学[107]、经济学[108]、商业[109]和TSP问题[110]。
2011年,Walton等人为CSA引入了一种变体,称为改进布谷鸟搜索(Modified Cuckoo Search, MCS),其主要目标是提高收敛速度[111]。这种增强涉及到一个额外的步骤,在这个步骤中,顶部的鸡蛋做一些信息共享。他们将MCS应用于多个基准函数,结果表明MCS的性能优于标准CSA。CSA的另一种流行变体是Layeb在2011年提出的量子启发布谷鸟搜索算法(Quantum Inspired Cuckoo Search Algorithm, QICSA)[112]。作者整合了量子位表示、测量运算、量子突变等量子计算原理中的元素。其主要目标是提高标准CSA的多样性和性能。结果表明,QICSA算法仍存在一些不足,作者建议将局部搜索和并行机器相结合,以提高效率和提高收敛速度[112]。
9. 其他进化算法
还有很多其他的进化算法,但是在前面几节中没有讨论,因为前面几节的目的只是介绍和讨论众所周知的、常用的基于si的方法。因此,本节主要讨论其他有趣的进化算法,如遗传规划(GP)、进化策略(ES)、进化规划(EP)、萤火虫算法(FA)、蝙蝠算法(BA)和灰狼优化器(GWO)。
GP是另一种进化算法,涉及与遗传算法类似的过程。GP使用术语程序,GA使用术语染色体来表示解。GP的程序从随机创建初始种群开始。之后,重复三个步骤,直到满足停止条件。这些步骤是健康评估、选择和繁殖。GP和GA的唯一区别在于选择过程。GA选择预定义的最适种群的百分比进行繁殖,而在GP中,每个程序根据分配给每个程序的概率(基于它们的适合度)从总体中选择一个或几个程序(根据目标)[113]。
ES算法是另一种优化方法,它使用与GA和DE相同的方法,但它使用自适应变异率。它有(1+1)-ES、(1+λ)-ES和(μ/ρ +, λ)-ES三种程序。(1+1)-ES的运作方式是,每个父母只产生一个突变(孩子),与那个父母竞争。突变体将成为下一代的父代,只有当它的表现与原始父代一样好。如果不是,则省略突变。在(1+λ)-ES中,生成λ突变体,选择最优突变体作为下一代的新亲本,忽略当前亲本的适合度。(μ/ρ +, λ)-ES是相当现代的,经常被用作标准ES。μ表示亲本种群中包含的个体数,ρ它是用于重组的确定的亲本个体数。因此,ρ应该等于或小于μ。λ表示每一代生育的子女数。注意,所有这些参数都是正整数。+,是决定使用“+”策略还是“逗号”策略的运算符。“加”策略忽略了个体的年龄,这意味着父母正在与他们的孩子竞争生存,并被购买给下一代。“逗号”策略是指父母总是被省略,新父母从最适合新一代的孩子中选择[114]。
EP与遗传算法的步骤相似,包括初始化、变异和评估操作。然而,EP和GA之间的主要区别是EP不使用任何交叉操作来生成子代或子代。EP和ES有很多相似之处。然而,它们有两个主要的区别,即选择和重组。EP通常使用随机选择,而ES使用确定性选择。随机选择意味着每个解与预定数量的其他解竞争,最不适合的解被淘汰。确定性选择是指在最坏的解决方案评估后直接剔除它们[115,116]。FA的灵感来自萤火虫的行为,它们通过闪烁的光相互吸引。FA在灵感方面与GSO算法非常相似。萤火虫的适合度将决定它们闪烁的亮度。这种亮度也会随着距离的增加而减少。不太亮的萤火虫会向更亮的萤火虫移动,如果没有更亮的萤火虫,这个特定的萤火虫会随机移动[117]。
Bat算法是另一种最近引入的优化技术。它是由Yang和Gandomi在2012年引入的,灵感来自于蝙蝠觅食的行为。该算法与PSO非常相似,由速度和位置方程组成[118,119]。由于该算法的灵感来自蝙蝠,它考虑了蝙蝠的回声定位能力,也利用了频率方程。这个频率方程直接影响到速度方程,而速度方程决定了搜索空间中的方向[118-120]。Mirjalili等人受到捕食者灰狼的启发,引入了GWO[121]。该算法将agent(灰狼)从上到下分别划分为alpha、beta、delta和omega几个层次。为了找到解决方案,每个层次都有不同的角色。请注意,还有很多进化算法未在本文中讨论,如文献[121]。
结论
本文关注各种基于群体智能(SI)的方法的总体性能。一套遗传算法(GA),蚁群优化(ACO),粒子群优化(PSO),差分进化(DE),人工蜂群(ABC),萤火虫群优化(GSO),和布谷鸟搜索算法(CSA)。DE算法在30个函数中有24个函数的性能优于或等同于最佳算法。DE在多模态函数上表现得非常好,在12个这样的函数中有11个被选为性能最好的方法。PSO是第二好的方法,在30个函数中有18个优于或等同于最好的算法,其次是GA,在30个函数中有14个,包括策略适应差分进化(SADE)[132],带有可选外部档案库的自适应差分进化(133)[134],基于对立点的差分进化(OBDE)[88],紧凑差分进化(cDE)[135],选择PSO (SPSO)[136],紧凑PSO[137],智能单粒子so (ISPSO)[138],和综合学习PSO (CLPSO)[139]。
参考文献
1. Bonabeau E, Dorigo M, Theraulaz G. Swarm Intelligence: From Natural to Artificial Systems. Journal of Artificial Societies and Social Simulation. 1999;4: 320.
2. Goldberg D. Genetic Algorithms in Optimization, Search and Machine Learning. Addison Wesley. 1987: 432.
3. Holland J, Genetic Algorithms. Scientific American Journal. 1992: 66–72.
4. Grefenstette JJ. GENESIS. Navy Center for Applied Research in Artificial Intelligence, Navy research Lab. 1990:.
5. Bhattacharjya RK. Introduction to Genetic Algorithms. IIT Guwahati. 2012, Available: http://www.iitg.ernet.in/rkbc/CE602/CE602/Genetic%20Algorithms.pdf. Accessed 14 November 2013.
6. Devooght R. Multi-objective genetic algorithm. 2010: 1–39. Available: epb-physique.ulb.ac.be/IMG/pdf/devooght_2011.pdf. Accessed 01 January 2014.
7. Uzel O, Koc E. Basic of Genetic Programming. Graduation Project I. 2012: 1–25. Available: http://mcs.cankaya.edu.tr/proje/2012/guz/omer_erdem/Rapor.pdf. Accessed 03 January 2014.
8. Filho MG, Barco CF, Neto RFT. Using Genetic Algorithms to solve scheduling problems on flexible manufacturing systems (FMS): a literature survey, classification and analysis. Flexible Services and Manufacturing Journal. 2014;26(3): 408–431.
9. Cheng C, Yang Z, Xing L, Tan Y. An improved genetic algorithm with local search for order acceptance and scheduling problems. IEEE Workshop on Computational Intelligence in Production and Logistics Systems (CIPLS). 2013: 115–122.
10. Sachdeva J, Kumar V, Gupta I, Khandelwal N, Ahuja CK. Multiclass Brain Tumor Classification Using GA-SVM. Developments in E-systems Engineering (DeSE). 2011: 182–187.
11. Khuntia AK, Choudhury BB, Biswal BB, Dash KK. A heuristics based multi-robot task allocation. Recent Advances in Intelligent Computational Systems (RAICS). 2011: 407–410.
12. Yang Q, Yu M, Liu S, Chai Z. Path planning of robotic fish based on genetic algorithm and modified dynamic programming. International Conference on Advanced Mechatronic Systems. 2011: 419–424.
13. Kang CC, Chuang YJ, Tung KC, Tang CY, Peng SC, Wong DS. A genetic algorithm-based Boolean delay model of intracellular signal transduction in inflammation. BMC Bioinformatics. 2011: 1–8.
14. Foschini L, Tortonesi M. Adaptive and business-driven service placement in federated Cloud computing environments. International Symposium on Integrated Network Management. 2013: 1245–1251.
15. Fu H, Li Z, Li G, Jin X, Zhu P. Modelling and controlling of engineering ship based on genetic algorithm. International Conference on Modelling, Identification & Control (ICMIC). 2012: 394–398.
16. Mahmudy WF, Marian RM, Luong LHS. Optimization of part type selection and loading problem with alternative production plans in flexible manufacturing system using hybrid genetic algorithms—part 1: Modelling and representation. International Conference on Knowledge and Smart Technology (KST). 2013: 75–80.
17. Mahmudy WF, Marian RM, Luong LHS. Optimization of part type selection and loading problem with alternative production plans in flexible manufacturing system using hybrid genetic algorithms—part 2: Genetic operators and results. International Conference on Knowledge and Smart Technology (KST). 2013: 81–85.
18. Jing X, Liu Y, Cao W. A Hybrid Genetic Algorithm for Route Optimization in Multimodal Transport. Fifth International Symposium on Computational Intelligence and Design (ISCID). 2012: 261–264.
19. ü?oluk G. Genetic algorithm solution of the TSP avoiding special crossover and mutation. Intelligent Automation & Soft Computing. 8. 2002: 265–272.
20. De Jong KA, Spears WM. A formal analysis of the role of multi-point crossover in genetic algorithms. Annals of Mathematics and Artificial Intelligence. 5. 1992: 1–26.
21. Chiao Mei FC, Phon-Amnuaisuk S, Alias MY, Leong PW. Adaptive GA: An essential ingredient in high-level synthesis. IEEE Congress on Evolutionary Computation. 2008: 3837–3844.
22. Raja PV, Bhaskaran VM. Improving the Performance of Genetic Algorithm by reducing the population size. International Journal of Emerging Technology and Advanced Engineering. 2013: 86–91.
23. Dorigo M. Optimization, learning and natural algorithms. Ph.D. Thesis, Politecnico di Milano, Milan. 1992. Available: http://ci.nii.ac.jp/naid/10016599043/
24. Dorigo M, Birattari M, Stutzle T. Ant Colony Optimization. Computational Intelligence Magazine, IEEE. 2006: 28–39.
25. Pei Y, Wang W, Zhang S. Basic Ant Colony Optimization. International Conference on Computer Science and Electronics Engineering. 2012: 665–667.
26. Abreu N, Ajmal M, Kokkinogenis Z, Bozorg B. Ant Colony Optimization. 2011: 1–26. Available: http://paginas.fe.up.pt/~mac/ensino/docs/DS20102011/Presentations/PopulationalMetaheuristics/ACO_Nuno_Muhammad_Zafeiris_Behdad.pdf. Accessed 28 December 2013.
27. Selvi V, Umarani R. Comparative Analysis of Ant Colony and Particle Swarm Optimization Techniques. International Journal of Computer Applications. 2010: 1–6.
28. Valdez F, Chaparro I. Ant Colony Optimization for solving the TSP symmetric with parallel processing. Joint IFSA World Congress and NAFIPS Annual Meeting. 2013: 1192–1196.
29. Tosuna U, Dokeroglua T, Cosara A. A robust Island Parallel Genetic Algorithm for the Quadratic Assignment Problem. International Journal of Production Research. 2013;51(14): 4117–4133.
30. Yagmahan B, Yenisey MM. A multi-objective ant colony system algorithm for flow shop scheduling problem. Expert Systems with Applications. 2010: 1361–1368.
31. Abdelaziz AY, Almoataz Y, Elkhodary SM, Osama RA. Distribution Networks Reconfiguration for Loss Reduction Using the Hyper Cube Ant Colony Optimization. International Conference on Computer Engineering & Systems. 2011: 79–84.
32. Kumar SB, Myilsamy G. Multi-target tracking in mobility sensor networks using Ant Colony Optimization. International Conference on Emerging Trends in Computing, Communication and Nanotechnology. 2013: 350–354.
33. Agrawal P, Kaur S, Kaur H, Dhiman A. Analysis and Synthesis of an Ant Colony Optimization Technique for Image Edge Detection. International Conference on Computing Sciences. 2012: 127–131.
34. Zhao J, Xian-Wen G, Liu J, Fu X. Improved ant colony optimization algorithm and its application for path planning of mobile robot in 3-D space. International Conference on Advanced Computer Control. 2010: 194–198.
35. Yufeng H, Qinghua Z, Jianye L, Guili X, Xiaoyi D. Path planning for indoor UAV based on Ant Colony Optimization. 25th Chinese Control and Decision Conference. 2013: 2919–2923.
36. Abdallah H, Emara HM, Dorrach HT, Bahgat A. Using Ant Colony Optimization Algorithm for Solving Project Management Problems. Expert Systems with Application. 2009: 10004–10015.
37. Dorigo M, Gambardella LM. Ant colony system: a cooperative learning approach to the traveling salesman problem. IEEE Transaction on Evolutionary Computation. 1. 1997: 53–66.
38. Stützle T, Hoos HH. MAX-MIN Ant System. Future Generation Computer System. 2000;16: 889–914.
39. Kennedy J, Eberhart R. Particle swarm optimization. IEEE International Conference on Neural Networks. 1995:1942–1948.
40. Del Valle Y, Venayagamoorthy GK, Mohagheghi S, Hernandez JC, Harley RG. Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power System. IEEE Trans Evolutionary Computer. 2008: 171–195.
41. Shi Y, Eberhart R. A modified particle swarm optimizer. IEEE World Congress on Computational Intelligence. 1998: 69–73.
42. Yan X, Wu Q, Liu H, Huang W. An Improved Particle Swarm Optimization Algorithm and Its Application. International Journal of Computer Science. 2013: 316–324.
43. Arumugam MS, Rao MVC, Tan AWC. A novel and effective particle swarm optimization like algorithm with extrapolation technique. Applied Soft Computing. 2009: 308–320.
44. Kiranyaz S, Ince T, Yildirim A, Gabbouj M. Fractional particle swarm optimization in multidimensional search space. IEEE Transactions on Systems, Man, and Cybernatics, Part B: Cybernatics. 2010: 298–319.
45. Gao H, Kwong S, Yang J, Cao J. Particle swarm optimization based on intermediate disturbance strategy algorithm and its application in multi-threshold image segmentation. Information Science. 2013: 1–31.
46. Banks A, Vincent J, Anyakoha C. A Review of Particle Swarm Optimization. Part I: Background and Development. Springer Science. 2007: 467–484.
47. Banks A, Vincent J, Anyakoha C. A Review of Particle Swarm Optimization. Part II: Hybridisation, Combinatorial, Multicriteria and Constrained Optimization, and Indicative Applications. Springer Science. 2007: 109–124.
48. Poli R, Kennedy J, Blackwell T. Particle Swarm Optimization an Overview. Swarm Intell. 2007: 1–25.
49. Gong D, Lu L, Li M. Robot Path Planning In Uncertain Environments Based On Particle Swarm Optimization. IEEE Congress on Evolutionary Computation. 2009: 2127–2134.
50. Bai Q. Analysis of Particle Swarm Optimization Algorithm. Computer and Information Science. 2010: 180–184.
51. Gong M, Cai Q, Chen X, Ma L. Complex Network Clustering by Multi-objective Discrete Particle Swarm Optimization Based on Decomposition. IEEE Transaction on Evolutionary Computation. 2014;18(1): 82–97.
52. Sivakumar P, Grace SS, Azeezur RA. Investigations on the impacts of uncertain wind power dispersion on power system stability and enhancement through PSO technique. International Conference on Energy Efficient Technologies for Sustainability. 2013: 1370–1375.
53. Li F, Li D, Wang C, Wang Z. Network signal processing and intrusion detection by a hybrid model of LSSVM and PSO. IEEE International Conference on Communication Technology. 2013: 11–14.
54. Jun Z, Kanyu Z. A Particle Swarm Optimization Approach for Optimal Design of PID Controller for Temperature Control in HVAC. International Conference on Measuring Technology and Mechatronics Automation. 2011: 230–233.
55. Atyabi A, Luerssen M, Fitzgibbon SP. Powers DMW, PSO-Based Dimension Reduction of EEG Recordings: Implications for Subject Transfer in BCI. Neurocomputing. Elsevier. 2013: 319–331.
56. Mohan S, Mahesh TR. Particle Swarm Optimization based Contrast Limited enhancement for mammogram images. International Conference on Intelligent Systems and Control. 2013: 384–388.
57. Gorai A, Ghosh A. Hue-preserving colour image enhancement using particle swarm optimization. Recent Advances in Intelligent Computational Systems. 2011: 563–568.
58. Na L, Yuanxiang L. Image Restoration Using Improved Particle Swarm Optimization. International Conference on Network Computing and Information Security. 2011: 394–397.
59. Chang Y, Yu G. Multi-Sub-Swarm PSO Classifier Design and Rule Extraction. Int. Work. Cloud Computing Information Security. 2013: 104–107.
60. Atyabi A, Powers DMW. Cooperative area extension of PSO: Transfer learning vs. uncertainty in a simulated swarm robotics. Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics. 2013: 177–184.
61. Shi YH, Eberhart RC. A modified particle swarm optimizer. Proceedings of the IEEE International Conference on Evolutionary Computation. 1998: 69–73.
62. Bratton D, Kennedy J. Defining a Standard for Particle Swarm Optimization. Proceedings of the IEEE Swarm Intelligence Symposium. 2007: 120–127.
63. Clerc M, Kennedy J. The Particle Swarm-Explosion, Stability, and Convergence in a Multidimensional Complex Space. IEEE Transactions on Evolutionary Computation 2002;6(1): 58–73.
64. Eberhart RC, Shi Y. Comparing inertia weights and constriction factors in particle swarm optimization. Proceedings of the Congress on Evolutionary Computation. 2000: 84–88.
65. Figueiredo EMN, Ludermir TB. Effect of the PSO Topologies on the Performance of the PSO-ELM. Brazilian Symposium on Neural Networks. 2012: 178–183.
66. Storn R, Price K. Differential Evolution—A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. Journal of Global Optimization. 1997: 341–359.
67. Price K, Storn R, Lampinen J. Differential Evolution: A Practical Approach to Global Optimization. Springer. 2005;104: 542.
68. Wu Y, Lee W, Chien C. Modified the Performance of Differential Evolution Algorithm with Dual Evolution Strategy. International Conference on Machine Learning and Computing. 2011: 57–63.
69. Dragoi E, Curteanu S, Vlad D. Differential evolution applications in electromagnetics. International Conference and Exposition on Electrical and Power Engineering. 2012: 636–640.
70. Myeong-Chun L, Sung-Bae C. Interactive differential evolution for image enhancement application in smart phone. IEEE Congress on Evolutionary Computation. 2012: 1–6.
71. Yilmaz AR, Yavuz O, Erkmen B. Training multilayer perceptron using differential evolution algorithm for signature recognition application. Signal Processing and Communications Applications Conference. 2013: 1–4.
72. Chiou J, Chang C, Wang C. Hybrid Differential Evolution for Static Economic Dispatch. International Symposium on Computer, Consumer and Control. 2014: 950–953.
73. Mezura-Montes E, Velazquez-Reyes J, Coello Coello CA. A Comparative Study of Differential Evolution Variants for Global Optimization. Proceedings of Genetic Evolutions Computation Conference. 2006: 332–339.
74. Das S, Suganthan PN. Differential evolution: A survey of the state-of-the-art. IEEE Transaction Evolutionary Computation 2011;15: 4–31.
75. Price KV. An Introduction to Differential Evolution. New Ideas in Optimization. Corne D, Dorigo M, Glover V, McGraw-Hill, UK. 1999: 79–108.
76. Karaboga D. An idea based on honeybee swarm for numerica optimization. Technical Report TR06. Erciyes University. 2005.
77. Karaboga D, Basturk B. A Powerful and Efficient Algorithm for Numeric Function Optimization: Artificial Bee Colony (ABC) Algorithm. Journal of Global Optimization. 2007: 459–471.
78. Karaboga D. Artificial bee colony algorithm. Scholarpedia. 2010: 6915.
79. Rao RS, Narasimham SVL, Ramalingaraju M. Optimization of distribution network configuration for loss reduction using artificial bee colony algorithm. International Journal of Electrical Power and Energy Systems Engineering. 2008: 116–122.
80. Singh A. An artificial bee colony algorithm for the leaf-constrained minimum spanning tree problem. Applied Soft Computing. 2009: 625–631.
81. Abu-Mouti FS, El-Hawary ME. Overview of Artificial Bee Colony (ABC) algorithm and its applications. International Systems Conference (SysCon). 2012: 1–6.
82. Gerhardt E, Gomes HM. Artificial Bee Colony (ABC) Algorithm for Engineering Optimization Problems. International Conference on Engineering Optimization. 2012: 1–11.
83. Sharma TK, Pant M. Golden Search Based Artificial Bee Colony Algorithm and Its Application to Solve Engineering Design Problems. International Conference on Advanced Computing & Communication Technologies. 2012: 156–160.
84. Chae-Ho L, Ji-Yong P, Jae-Yong P, Seog-Young H. Application of artificial bee colony algorithm for structural topology optimization. International Conference on Natural Computation. 2012: 1023–1025.
85. Ting-En L, Jao-Hong C, Lai-Lin J. A New Artificial Bee Colony Based Clustering Method and Its Application to the Business Failure Prediction. International Symposium on Computer, Consumer and Control. 2012: 72–75.
86. Karaboga D, Gorkemli B, Ozturk C, Karaboga N. A comprehensive survey: artificial bee colony (ABC) algorithm and applications. Artificial Intelligence Review. 2014;42(1): 21–57.
87. Bolaji AL, Khader AT, Al-Betar MA, Awadallah MA. Artificial bee colony algorithm, its variants and applications: A survey. Journal of Theoretical Applied Information Technology. 2013;47: 434–459.
88. Bao LBL, Zeng JZJ. Comparison and Analysis of the Selection Mechanism in the Artificial Bee Colony Algorithm. International Conference on Hybrid Intelligent System. 2009: 411–416.
89. Krihnanand KN, Ghose D. Glowworm Swarm Optimization for Simultaneous Capture of Multiple Local Optima of Multimodal Functions. Journal of Swarm Intelligence. 2009: 87–124.
90. Krihnanand KN, Ghose D. Glowworm Swarm Optimization: A new method for optimizing multi-modal function. Journal of Computational Intelligence Studies. 2009: 93–119.
91. Krihnanand KN, Amruth P, Guruprasad MH. Glowworm-inspired Robot Swarm for Simultaneous Taxis towards Multiple Radiation Sources. International Conference on Robotics and Automation. 2006: 958–963.
92. Zainal N, Zain AM, Radzi NHM, Udin A. Glowworm Swarm Optimization (GSO) Algorithm for Optimization Problems: A State-of-the-Art Review. Applied Mechanics and Materials. 2013;421: 507–511.
93. Yuli Z, Xiaoping MA, Yanzi MIAO. Localization of Multiple Odor Source Using Modified Glowworm Swarm Optimization with Collective Robots. Proceeedings of the 30th Chinese Control Conference. 2011: 1899–1904.
94. Deng-Xu H, Hua-Zheng Z, Gui-Qing L. Glowworm swarm optimization algorithm for solving multi-constrained QoS multicast routing problem. International Conference on Computational Intelligence and Security. 2011: 66–70.
95. Krishnanand KN, Ghose D. Detection of multiple source locations using a glowworm metaphor with applications to collective robotics. Proceedings Swarm Intelligence Symposium. 2005: 84–91.
96. Senthilnath J, Omkar SN, Mani V, Tejovanth N, Diwakar PG, Archana BS. Multi-spectral satellite image classification using Glowworm Swarm Optimization. International Geoscience and Remote Sensing Symposium. 2011: 47–50.
97. McGill K, Taylor S. Comparing swarm algorithms for large scale multi-source localization. International Conference on Technologies for Practical Robot Applications. 2009: 48–54.
98. Menon PP, Ghose D. Simultaneous source localization and boundary mapping for contaminants. American Control Conference. 2012: 4174–4179.
99. He L, Tong X, Huang S. A Glowworm Swarm Optimization Algorithm with Improved Movement Rule. Fifth International Conference on Intelligent Networks and Intelligent Systems. 2012: 109–112.
100. Zhang YL, Ma XP, Gu Y, Miao YZ. A modified glowworm swarm optimization for multimodal functions. Chinese Control and Decision Conference (CCDC). 2011: 2070–2075.
101. Zhao G, Zhou Y, Wang Y. The Glowworm Swarm Optimization Algorithm with Local Search Operator. Journal of Information & Computational Science. 2012: 1299–1308.
102. Yang XS, Deb S. Cuckoo Search via Levy Flights. World Congress on nature and biologically inspired computing (NaBIC). 2009: 210–214.
103. Yang XS, Deb S. Engineering optimization by cuckoo search. Int. J. Mathematical Modelling and Numerical Optimization. 2009: 330–343.
104. Yang XS, Deb S. Multi-objective cuckoo search for design optimization. Computer Operations Research. 2013: 1616–1624.
105. Chaowanawatee K, Heednacram A. Implementation of Cuckoo Search in RBF Neural Network for Flood Forecasting. International Conference on Computational Intelligence, Communication Systems and Networks. 2012: 22–26.
106. Kumar A, Chakarverty S. Design optimization for reliable embedded system using Cuckoo Search. International Conference on Electronics Computer Technology. 2011: 264–268.
107. Khodier M. Optimisation of antenna arrays using the cuckoo search algorithm. Microwaves, Antennas & Propagation. 2013: 458–464.
108. Vo DN, Schegner P, Ongsakul W. Cuckoo search algorithm for non-convex economic dispatch. Generation, Transmission & Distribution. 2013: 645–654.
109. Yang XS, Deb S, Karamanoglu M, Xingshi N. Cuckoo search for business optimization applications. National Conference on Computing and Communication Systems. 2012: 1–5.
110. Jati GK, Manurung HM, Suyanto S. Discrete cuckoo search for traveling salesman problem. International Conference on Computing and Convergence Technology. 2012: 993–997.
111. Walton S, Hassan O, Morgan K, Brown MR. Modified cuckoo search: A new gradient free optimisation algorithm. Chaos, Solitons and Fractals. 2011;44: 710–718.
112. Layeb A, Boussalia SR. A Novel Quantum Inspired Cuckoo Search Algorithm for Bin Packing Problem. International Journal of Information Technology and Computer Science. 2012;4: 58–67.
113. Poli R, Langdon W, McPhee N, Koza J. A Field Guide to Genetic Programming. 2008. Available: http://dces.essex.ac.uk/staff/rpoli/gp-field-guide/A_Field_Guide_to_Genetic_Programming.pdf on 1 November 2014.
114. Hansen N, Arnold DV, Auger A. Evolution Strategies. 2013: 1–35. Retrieved from https://www.lri.fr/~hansen/es-overview-2014.pdf. Accessed 1 November 2014.
115. Fogel GB, Fogel D, Fogel L. Evolutionary Programming. Scholarpedia. 2011;6(4): 1818.
116. B?ck T, Rudolph G, Schwefel HP. Evolutionary Programming and Evolution Strategies: Similarities and Differences. In Proceedings of the Second Annual Conference on Evolutionary Programming. 1993: 11–22.
117. Yang XS. Firefly algorithms for multimodal optimization. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics). 2009;5792: 169–178.
118. Yang XS, Gandomi AH. Bat Algorithm: A Novel Approach for Global Engineering Optimization. Engineering Computations. 2012;29(5): 464–483. pmid:22622488
119. Yang XS. Bat Algorithm for Multiobjective Optimization. International Journal on Bio-Inspired Computation. 2011;3: 267–274.
120. Yang XS. Bat Algorithm: Literature Review and Applications. Int. J. Bio-Inspired Computation. 2013;5: 10.
121. Marjalili S, Mirjalili SM, Lewis A. Grey Wolf Optimizer. Advances in Engineering Software. 2014: 46–61.
122. Fernando GL, Lima CF, Michalewicz Z. Parameter Setting in Evolutionary Algorithms. Studies in Computitional Intelligence. Springer. 2007
123. Parapar J, Vidal MM, Santos J. Finding the Best Parameter Setting: Particle Swarm Optimisation. 2nd Spanish Conference on Information Retrieval. 2012: 49–60.
124. Zhang L, Yu H, Hu S. Optimal choice of parameters for particle swarm optimization. Journal of Zhejiang University Science, 2005: 528–534.
125. Josef T. Differential Evolution: Competitive Setting of Control Parameters. Proceedings of the International Multiconference on Computer Science and Information Technology. 2006: 207–213.
126. Zhang H, Fu P, Liu Y. Parameter Setting Analysis for Glowworm Swarm Optimization Algorithm. Journal of Information & Computational Science. 2012: 3231–3240.
127. Akay B, Karaboga D. Parameter Tuning for the Artificial Bee Colony Algorithm. Computational Collective Intelligence. Semantic Web, Social Networks and Multiagent Systems Lecture Notes in Computer Science. 2009: 608–619.
128. Gaertner D, Clark K. On Optimal Parameters for Ant Colony Optimization Algorithms. Proceedings of the International Conference on Artificial Intelligence. 2005: 85–89.
129. Stützle T, López-Ibá?ez M, Pellegrini P, Maur M, de Oca MM, Birattari M, et al. Parameter Adaptation in Ant Colony Optimization. Autonomous Search. 2012: 191–215.
130. Jamil M, Yang XS. A literature survey of benchmark functions for global optimization problems. Int. Journal of Mathematical Modelling and Numerical Optimisation. 2013;4(2): 150–194.
131. Dieterich JM, Hartke B. Empirical review of standard benchmark functions using evolutionary global optimization. 2012. Avaialble: http://arxiv.org/pdf/1207.4318.pdf. Accessed 15 October 2014.
132. Qin AK, Huang VL, Suganthan PN. Differential evolution algorithm with strategy adaptation for global numerical optimization. IEEE Transactions on Evolutionary Computation. 2009: 398–417.
133. Zhang J, Sanderson AC. JADE: Adaptive differential evolution with optional external archive. IEEE Transactions on Evolutionary Computation. 2009: 945–958.
134. Rahnamayan S, Tizhoosh H, Salama M. Opposition-based differential evolution. IEEE Transaction on evolutionary computation. 2008: 64–79.
135. Mininno E, Neri F, Cupertino F, Naso D. Compact Differential Evolution. IEEE Transactions on Evolutionary Computation. 2011: 32–54.
136. Angelinne P. Using Selection to Improve Particle Swarm Optimization. IEEE International Conference on Evolutionary Computation. 1998: 84–90.
137. Neri F, Mininno E, Iacca G. Compact Particle Swarm Optimization. Information Science. 2013: 96–121.
138. Zhou J, Ji Z, Shen L. Simplified intelligence single particle optimization based neural network for digit recognition. Proceedings of the Chinese Conference on Pattern Recognition. 2008: 1–5.
139. Liang JJ, Qin AK, Suganthan PN, Baskar S. Comprehensive learning particle swarm optimization for global optimization of multimodal functions. IEEE Transaction on Evolutionary Computational. 2006: 281–295.
140. Karaboga D, Akay B. A comparative study of Artificial Bee Colony algorithm. Applied Mathematics and Computation. 2009: 108–132.
141. Civicioglu P, Besdok E. A conceptual comparison of cuckoo-search, particle swarm optimization, differential evolution and artificial bee colony algorithm. Artificial Intelligence Review, Springer. 2013: 315–346.
142. Zhao G, Zhou Y, Wang Y. The Glowworm Swarm Optimization Algorithm with Local Search Operator. Journal of Information & Computational Science. 2012: 1299–1308.
143. Wang X, Gao XZ, Ovaska SJ. A Hybrid Optimization Algorithm Based on Ant Colony and Immune Principles. International Journal of Computer Science & Application. 2007: 30–44.
144. Venkata R, Patel V. An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems. Transactions D: Computer Science & Engineering and Electrical Engineering. 2013: 710–720.
145. Goudos SK, Baltzis KB, Antoniadis K, Zaharis ZD, Hilas CS. A Comparative Study of Common and Self-Adaptive Differential Evolution Strategies on Numerical Benchmark Problems. Procedia Computer Science. 2011: 83–88.
146. Ghosh S, Das S, Kundu D, Suresh K, Abraham A. Inter-particle communication and search dynamics of lbest partice swarm optimizers: an analysis. Information Science. 2012: 156–168.
147. Niwa J. Glowworm optimization. International Conference on Swarm and Evolutionary Computation. Springer-Verlag. 2012: 310–316.
148. Xu G. An adaptive parameter tuning of particle swarm optimization algorithm. Applied Mathematics and Computation. 2013: 4560–4569.
149. Iranpour B, Meybodi M. An Improved Fuzzy Based Glowworm Algorithm. International Journal of Engineering and Technology. 2012: 900–905.
150. Liao T, Molina D, Stutzle T, Oca MAM, Dorigo M. An ACO algorithm benchmarked on the BBOB noiseless function testbed. International Conference on Genetic and Evolutionary Computation Conference Companion. 2012: 159–166.
151. Liao T, Oca MAM, Aydin D, Stutzle T, Dorigo M. An Incremental Ant Colony Algorithm with Local Search for Continuous Optimization. Genetic and Evolutionary Computation Conference. 2011: 125–132.
152. Socha K, Dorigo M. Ant colony optimization for continuous domains. European Journal of Operational Research. 2008: 1155–1173.
153. Maniezzo V, Gambardella LM, Luigi F. Ant Colony Optimization. 2001: 1–21. Available: http://www.cs.unibo.it/bison/publications/ACO.pdf. Accessed 02 December 2013.
154. Wu B, Qian C, Ni W, Fan S. The improvement of glowworm swarm optimization for continuous optimization problems. Expert Systems with Applications. 2012: 6335–6342.
155. Hansen N, Kern S. Evaluating the CMA Evolution Strategy on Multimodal Test Functions. Parallel Problem Solving from Nature—PPSN VIII. 2004;3242: 282–291.
156. Ma T, Yan Q, Xuan W, Wang B. A Comparative Study of Quantum Evolutionary Algorithm and Particle Swarm Optimization for Numerical Optimization Problems. International Journal of Digital Content Technology and its Applications. 2011;5(7): 182–190.
157. Devi S, Jadhav DG, Pattnaik SS. PSO Based Memetic Algorithm for Unimodal and Multimodal Function Optimization. SEMCCO, Part 1. 2011: 127–134.
158. Simon D. Evolutionary Optimization Algorithms: Biologically-Inspired and Population-Based Approaches to Computer Intelligence. 2013. Available: http://academic.csuohio.edu/simond/EvolutionaryOptimization/. Accessed 05 December 2014.
159. Mirjalili S. Biogeography-Based Optimizer (BBO) for training Multi-Layer Perceptron (MLP). 09 March 2014. Available: Biogeography-Based Optimizer (BBO) for training Multi-Layer Perceptron (MLP). Accessed 05 December 2014.
160. Yang XS. Cuckoo Search (CS) Algorithm. 22 December 2010 Available: Cuckoo Search (CS) Algorithm. Accessed 05 December 2014.
161. Karaboga D, Akay B. Artificial Bee Colony (ABC), Harmony Search and Bees Algorithms on Numerical Optimization. 14 December 2009. Available: http://mf.erciyes.edu.tr/abc/software.htm. Accessed 05 December 2014
在确定了训练集、假设空间
以及学习准则后,如何找到最优的模型
就成了一个最优化(Optimization)问题.机器学习的训练过程其实就 是最优化问题的求解过程.
参数与超参数 在机器学习中,优化又可以分为参数优化和超参数优化.模型中的
称为模型的参数,可以通过优化算法进行学习.除了可学习的参数
之外,还有一类参数是用来定义模型结构或优化策略的,这类参数叫作超参数(Hyper-Parameter)
常见的超参数包括:聚类算法中的类别个数、梯度下降法中的步长、正则化项的系数、神经网络的层数、支持向量机中的核函数等.超参数的选取一般都是组合优化问题,很难通过优化算法来自动学习.因此,超参数优化是机器学习的一个经验性很强的技术,通常是按照人的经验设定,或者通过搜索的方法对一组超参数组合进行不断试错调整.
为了充分利用凸优化中一些高效、成熟的优化方法,比如共轭梯度、拟牛顿法等,很多机器学习方法都倾向于选择合适的模型和损失函数,以构造一个凸函数作为优化目标。但也有很多模型(比如神经网络)的优化目标是非凸的,只能退而求其次找到局部最优解.
在机器学习中,最简单、常用的优化算法就是梯度下降法,即首先初始化参数,然后按下面的迭代公式来计算训练集
上风险函数的最小值:
其中为第
次迭代时的参数值 ,
为搜索步长.在机器学习中,一般称为学习率(Learning Rate).
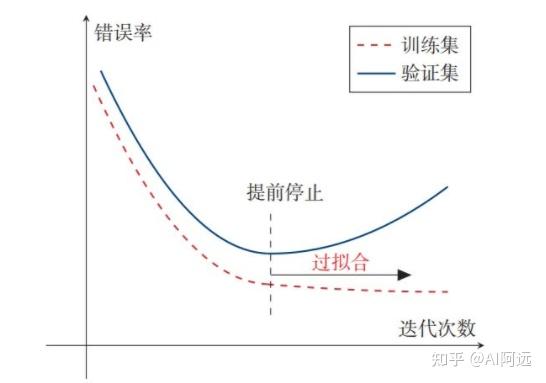
针对梯度下降的优化算法,除了加正则化项之外,还可以通过提前停止来防止过拟合.在梯度下降训练的过程中,由于过拟合的原因,在训练样本上收敛的参数,并不一定在测试集上最优.
因此,除了训练集和测试集之外, 有时也会使用一个验证集(Validation Set)来进行模型选择,测试模型在验证集上是否最优.验证集也叫作开发集(Development Set).在每次迭代时,把新得到的模型 在验证集上进行测试,并计算错误率.如果在验证集上的错误率不再下降,就停止迭代.
这种策略叫提前停止(EarlyStop).如果没有验证集,可以在训练集上划分出一个小比例的子集作为验证集.
下图给出了提前停止的示例
在梯度下降法中,目标函数是整个训练集上的风险函数,这种方式称为批量梯度下降法(Batch Gradient Descent,BGD). 批量梯度下降法在每次迭代时需要计算每个样本上损失函数的梯度并求和.当训练集中的样本数量很大时,空间复杂度比较高,每次迭代的计算开销也很大.
在机器学习中,我们假设每个样本都是独立同分布地从真实数据分布中随机抽取出来的, 真正的优化目标是期望风险最小.批量梯度下降法相当于是从真实数据分布中采集个样本,并由它们计算出来的经验风险的梯度来近似期望风险的梯度.为了减少每次迭代的计算复杂度,我们也可以在每次迭代时只采集一个样本,计算这个样本损失函数的梯度并更新参数,即随机梯度下降法(Stochastic Gradient Descent,SGD).随机梯度下降法也叫作增量梯度下降法.当经过足够次数的迭代时,随机梯度下降也可以收敛到局部最优解.
随机梯度下降法的训练过程如下所示:

批量梯度下降和随机梯度下降之间的区别在于 ,每次迭代的优化目标是对所有样本的平均损失函数还是对单个样本的损失函数.由于随机梯度下降实现简单,收敛速度也非常快,因此使用非常广泛.随机梯度下降相当于在批量梯度下降的梯度上引入了随机噪声.在非凸优化问题中,随机梯度下降更容易逃离局部最优点。
随机梯度下降法的一个缺点是无法充分利用计算机的并行计算能力.小批量梯度下降法(Mini-Batch Gradient Descent)是批量梯度下降和随机梯度下降的折中.每次迭代时,我们随机选取一小部分训练样本来计算梯度并更新参数,这样既可以兼顾随机梯度下降法的优点,也可以提高训练效率。
第次迭代时,随机选取一个包含
个样本的子集
(
通常不会设置很大,一般在1-100之间),计算这个子集上每个样本损失函数的梯度并进行平均,然后再进行参数更新:
在实际应用中,小批量随机梯度下降法有收敛快、计算开销小的优点,因此逐渐成为大规模的机器学习中的主要优化算法.